In the world of algebra, equations can sometimes feel like cryptic messages from another dimension. Take the equation 12y – 20y = 16 for instance. At first glance, it might seem like a puzzle designed to confuse even the most seasoned math enthusiasts. But fear not! This equation is more than just a jumble of letters and numbers; it’s an invitation to uncover the beauty of solving for ‘y’ in a way that even your calculator would applaud.
Table of Contents
ToggleOverview of 12y–20y=16
The equation 12y – 20y = 16 simplifies to a linear form that reveals key properties of algebra. First, combine like terms on the left side: 12y minus 20y results in -8y. This leads to the simplified equation: -8y = 16.
Next, isolating y becomes essential. Divide both sides by -8 to solve for y, which results in y = -2. Efforts to solve linear equations often follow this straightforward approach, demonstrating the importance of careful arithmetic.
Each step in this equation showcases the process of moving terms to one side to isolate the variable. Clarity emerges as terms combine and are simplified, making it easier to find solutions. Understanding how to manipulate equations empowers individuals to handle more complex algebraic challenges later on.
Solutions derived from linear equations frequently serve as a foundation for different areas in mathematics. Engaging with algebraic expressions enriches problem-solving skills while fostering a deeper comprehension of mathematical principles.
Emphasizing step-by-step methods ensures readers grasp concepts effectively. This equation illustrates the relationship between coefficients and constants in algebra, highlighting their role during the solving process. Such clarity lays the groundwork for tackling a variety of algebraic phenomena, reinforcing the essential nature of these mathematical techniques.
Understanding the Equation
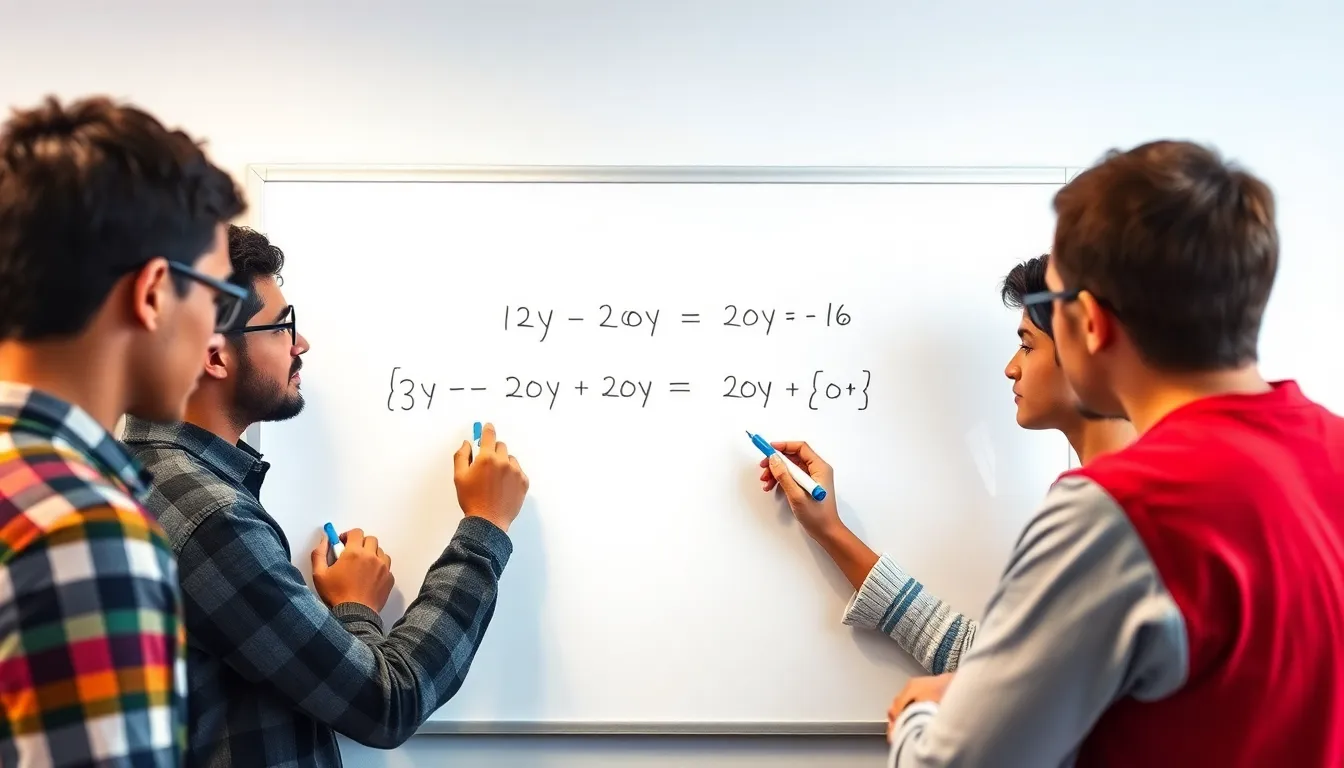
This section delves into the specifics of the equation 12y – 20y = 16. It breaks down each component for better clarity.
Components of the Equation
The equation consists of several essential parts. Coefficients such as 12 and -20 represent the numerical factors of ‘y’. The term -20y indicates subtraction, showing that the quantity decreases. A constant, 16, appears on the right side of the equation, providing a value that results from the algebraic manipulation. Combining like terms leads to -8y, simplifying the equation. This step underscores the relationship between variables and constants, highlighting how they interact within the equation. Understanding these components serves as a foundation for solving algebraic problems.
Importance of ‘y’ in the Equation
The variable ‘y’ plays a crucial role in the equation. Isolating ‘y’ allows for finding its value, which is essential for understanding the equation’s solution. The manipulation and simplification of terms center around ‘y’, demonstrating its significance in algebraic expressions. This variable not only represents an unknown quantity but also serves as a pivotal point in equations. Recognizing the importance of ‘y’ enhances problem-solving skills in algebra, enabling individuals to tackle more advanced mathematical concepts. As a variable, ‘y’ connects various algebraic equations and contributes to a comprehensive grasp of linear relationships in mathematics.
Solving 12y–20y=16
Solving the equation 12y – 20y = 16 involves isolating the variable ‘y’. This process starts with combining like terms.
Step-by-Step Solution
- Combine like terms: 12y and -20y together simplify to -8y.
- Rewrite the equation: Now, it reads as -8y = 16.
- Divide both sides by -8: This step isolates ‘y’, yielding y = -2.
These calculations illustrate a clear path to finding the value of ‘y’. Each step flows logically to reinforce understanding.
Common Mistakes to Avoid
- Forgetting to combine like terms can lead to incorrect coefficients.
- Misapplying division affects the solution negatively.
- Not checking the final answer against the original equation may cause oversight.
Avoiding these pitfalls ensures clarity and accuracy in solving algebraic equations. Prioritizing meticulous calculations will strengthen confidence in algebraic problem-solving.
Applications of the Equation
The equation 12y – 20y = 16 serves as a valuable tool for understanding various real-world applications.
Real-World Examples
In finance, individuals can use similar equations to calculate profit margins. Businesses frequently apply such calculations to determine pricing strategies. For instance, if a company sells products with differing costs, it can assess revenue by solving equations that represent profit losses or gains. Engineers also encounter this type of equation when analyzing force and motion in mechanical systems. These examples illustrate how algebra plays a critical role in daily decision-making processes across different professions.
Practical Uses in Different Fields
In education, the equation finds relevance in teaching foundational algebra concepts. Educators utilize it to demonstrate how to manipulate equations for students’ comprehension. Practicing with similar problems helps learners strengthen their problem-solving skills. Moreover, scientists use algebraic equations to model relationships in experiments, predicting outcomes through calculated variables. Mathematics also underpins economic analyses, where variables represent dynamic factors affecting market trends. Hence, this equation encapsulates essential skills applicable across diverse academic and professional fields.
Solving the equation 12y – 20y = 16 illustrates the fundamental principles of algebra. By simplifying the equation to -8y = 16 and isolating ‘y’, one can uncover the value of -2. This process not only emphasizes careful arithmetic but also enhances problem-solving skills essential in various fields.
Understanding the implications of such equations extends beyond academics. It equips individuals with tools to tackle real-world challenges in finance, engineering, education, and science. Mastering these concepts fosters confidence and clarity in mathematical reasoning, making algebra a vital skill in everyday decision-making.





